Generate Bitcoin Private Key Offline

Posted on 15.12.2020 by admin

sor41ng.netlify.app › 〓 Generate Bitcoin Private Key Offline 〓

How To Generate Bitcoin Private Key
Generate Bitcoin Private Key
Bitcoin Private Key With Balance
Generate Bitcoin Private Key Offline Free

What is a Bitcoin private key?

A paper wallet is a paper copy of your public and private key for your Bitcoins. Because they’re completely offline, paper wallets are one of the most secure ways to hold Bitcoins when done correctly. The advantage is that your private key is not stored digitally, so it isn’t subject to hacking. Making a paper. A tool for converting BIP39 mnemonic phrases to addresses and private keys. Enter your BIP39 phrase into the 'BIP39 Phrase' field, or press 'Generate Random Phrase'. You can save this page, turn off internet and generate private keys as lot as you wish.

A Bitcoin private key is a secret number which every Bitcoin wallet has. This 256-bit number can be represented in several formats: in hexadecimal – 256 bits, in hexadecimal is 32 bytes, or 64 characters in the range 0-9 or A-F, Base64 string, a WIF key, or a mnemonic phrase.

Here is an example:

E9873D79C6D87DC0FB6A5778633389F4453213303DA61F20BD67FC233AA33262

First method

The simplest way of generating a 32-byte integer is to use an RNG library in the language you know. Here are a few examples in Python:

bits = random.getrandbits(256)

# 30848827712021293731208415302456569301499384654877289245795786476741155372082

bits_hex = hex(bits)

# 0x4433d156e8c53bf5b50af07aa95a29436f29a94e0ccc5d58df8e57bdc8583c32

private_key = bits_hex[2:]

# 4433d156e8c53bf5b50af07aa95a29436f29a94e0ccc5d58df8e57bdc8583c32

However, normal RNG libraries are not the most secure options of generating a key. As the generated string is based on a seed, the seed represents the current time. And if you know the time, several brute-force attacks can be applied to it.

Cryptographically strong RNG

In addition to a standard RNG method, Programming languages provide a RNG for specific cryptographic tasks. As the entropy is generated directly from the operating system, this method ensures more security.

It makes this RNG more difficult to reproduce as you can’t determine the time of generation or the seed because it lacks one. No seed is required as it’s created by the program itself.

In Python, you can implement the cryptographically strong RNG in the secret module.

bits = secrets.randbits(256)

# 46518555179467323509970270980993648640987722172281263586388328188640792550961

bits_hex = hex(bits)

# 0x66d891b5ed7f51e5044be6a7ebe4e2eae32b960f5aa0883f7cc0ce4fd6921e31

private_key = bits_hex[2:]

# 66d891b5ed7f51e5044be6a7ebe4e2eae32b960f5aa0883f7cc0ce4fd6921e31

Specialized sites

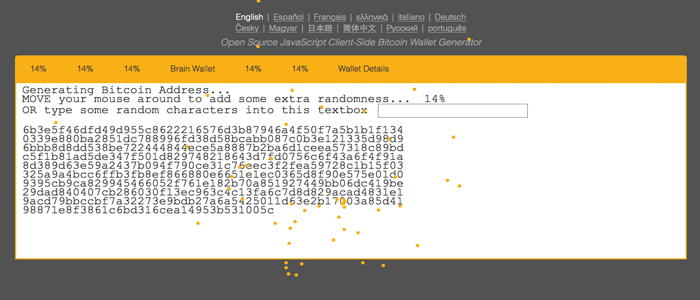
There are several sites which can generate these numbers randomly for you. Random.org is a site which randomly generates numbers for various purposes. Another popular site is bitaddress.org specifically designed to generate Bitcoin private keys.

As you have no way of knowing if random.org keeps or records any of the generated numbers, it is not such a secure option.

Bitaddress.org, however, is an open source, which means you can check its code to see what it does, and you can also download and run it on your computer in offline mode.

The program uses your mouse or key movements to generate entropy. This makes it highly improbable to reproduce your results.

Then, the private key is delivered in a compressed WIF format, but we will make the algorithm return a hex string which will be required later on for a public key generation.

Bitaddress first initializes a byte array, trying to get as much entropy as possible from your computer. It fills the array with the user input, and then it generates a private key. The service uses the 256-byte array to store entropy. This array is filled in cycles, so when the array is filled for the first time, the pointer resets to zero, the array is filled out again.

After an array is initiated from Window.crypto, it writes a timestamp to generate 4 additional bytes of entropy. It collects data such as the size of the screen, your time zone, information about browser plugins, your locale, among others to add another 6 bytes.

Then after initialization, the program repeatedly waits for the user input to rewrite initial bytes. When the cursor is moved, the position of the cursor is written. When buttons are pressed, the char code of the pressed button is written by the program.

The accumulated entropy to generate a private key of 32 bytes by using an RNG algorithm is called ARC4.

The DIY Version

Rsa key generator modulus exponent. You can also create your own version of Bitaddress. We will not be gathering data regarding the user’s computer and location. The entropy will be generated only by text, as it’s rather difficult to initialize a position of the cursor via a Python script.

The byte array will be initialized with a cryptographic RNG, then the timestamp will be filled, followed by the filling with a user-generated string.

After filling the second seed pool, the library will allow you to create the key.

Initializing the pool

We insert several bytes from cryptographic RNG and a timestamp. __seed_int and __seed_byte are two methods that will help insert the entropy into the pool array. We will also use the secrets module in our example.

def __init_pool(self):

for i in range(self.POOL_SIZE):

random_byte = secrets.randbits(8)

self.__seed_byte(random_byte)

time_int = int(time.time())

self.__seed_int(time_int)

def __seed_int(self, n):

self.__seed_byte(n)

self.__seed_byte(n >> 8)

self.__seed_byte(n >> 16)

self.__seed_byte(n >> 24)

def __seed_byte(self, n):

self.pool[self.pool_pointer] ^= n & 255

self.pool_pointer += 1

if self.pool_pointer >= self.POOL_SIZE:

self.pool_pointer = 0

Here, we insert a timestamp and then we input each character of the string.

def seed_input(self, str_input):

time_int = int(time.time())

self.__seed_int(time_int)

for char in str_input:

char_code = ord(char)

self.__seed_byte(char_code)

Generating the private key

In order to generate a 32-byte number with our pool, we have to use a shared object that is employed by any code that is running in one script.

To save our entropy each time a key is generated, the state we stopped at will be remembered and set for the next time a key will be generated.

Now we just need to ensure that our key is in range (1, CURVE_ORDER), which is required for ECDSA private keys. The CURVE_ORDER is the secp256k1 curve’s order.

We will be converting the key to hex, and remove the ‘0x’ part.

def generate_key(self):

How To Generate Bitcoin Private Key

big_int = self.__generate_big_int()

big_int = big_int % (self.CURVE_ORDER — 1) # key < curve order

big_int = big_int + 1 # key > 0

key = hex(big_int)[2:]

return key

def __generate_big_int(self):

if self.prng_state is None:

seed = int.from_bytes(self.pool, byteorder=’big’, signed=False)

random.seed(seed)

self.prng_state = random.getstate()

random.setstate(self.prng_state)

big_int = random.getrandbits(self.KEY_BYTES * 8)

self.prng_state = random.getstate()

return big_int

In order to use the library, you can generate a private key using the following code: